Lenny Counundrum # 111
Wed Mar 30, 2005 11:20 pm
Congratulations! You have guessed correctly in the Lenny Conundrum game (Round 110). We have given you a Thistleberry Crepe, an Avatar, and 517 NP!
Wed Mar 30, 2005 11:34 pm
I got it too.  But I'm suspended, so I can't see if I won the crepe.
But I'm suspended, so I can't see if I won the crepe. 
Wed Mar 30, 2005 11:36 pm
Uh..... The Bronze Trophy replaced my Silver one..... O_O
Thu Mar 31, 2005 12:27 am
I FINALLY got the avatar!
Thu Mar 31, 2005 1:57 am
Kinda sad that I missed being one of the first 250, I really want the avatar. That'll teach me to go to the grocery store on a Thursday!
Thu Mar 31, 2005 3:00 am
I didn't bother with this one. I hate math. 
Does someone want to post the answer?
Does someone want to post the answer?
Thu Mar 31, 2005 4:05 am
I got the item too... *wonders why they say you got an avatar even though ive won it 7 times now*.
Still only a bronze trophey though
Still only a bronze trophey though
Thu Mar 31, 2005 4:21 am
The answer was 132 people, Cranberry 
Thu Mar 31, 2005 9:27 am
Thanks! I got the trophy and avatar! My first win, I'm dead pleased!
Thu Mar 31, 2005 5:01 pm
No trig was necessary...
All that was needed was a calculator and a ruler to draw two straight lines!
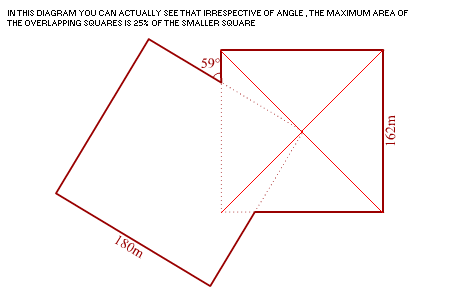
As you can see in the above diagram I drew two diagonals on the smaller square.
As the the corner of the larger square is at the centre of the smaller square, the MAXIMUM area of overlap is 25% (one-quarter of the smaller square).
Given the sides of each square, calculate the area of each. Calculate 25% of the area of the SMALLER square to find area of the overlapping area. Convert each area to minutes.
(Total minutes 189054 = 3150.9 hours)
(Divide by 8hrs*3days = 131.2875 people and round up)
All that was needed was a calculator and a ruler to draw two straight lines!

As you can see in the above diagram I drew two diagonals on the smaller square.
As the the corner of the larger square is at the centre of the smaller square, the MAXIMUM area of overlap is 25% (one-quarter of the smaller square).
Given the sides of each square, calculate the area of each. Calculate 25% of the area of the SMALLER square to find area of the overlapping area. Convert each area to minutes.
(Total minutes 189054 = 3150.9 hours)
(Divide by 8hrs*3days = 131.2875 people and round up)
Thu Mar 31, 2005 6:48 pm
That was perfectly described Gemma! In my mind, I 'cut' the bottom overlap of the smaller area and 'pasted' it on the top to form a triangle that is 1/4 the size of the smaller square.
Thu Mar 31, 2005 9:59 pm
New one is up, and I'm not even gonna bother trying it. 
Bartleby the Skeith was bored one morning, and decided to pull out an empty Armada board and some Armada pieces. He filled the entire board with random Armada pieces, one in each space. Then, he emptied the whole board and did it again. And then again, and then again. He decided to keep doing it until he filled the board with every possible combination of pieces.
If it takes him 30 seconds to set up and then empty the board each time, how long will it take him to set up every possible combination? Please round to the nearest year.
(Did quite a few of these kind of questions - in a much smaller version, of course - in math these few days so completely SICK of it.)
Bartleby the Skeith was bored one morning, and decided to pull out an empty Armada board and some Armada pieces. He filled the entire board with random Armada pieces, one in each space. Then, he emptied the whole board and did it again. And then again, and then again. He decided to keep doing it until he filled the board with every possible combination of pieces.
If it takes him 30 seconds to set up and then empty the board each time, how long will it take him to set up every possible combination? Please round to the nearest year.
(Did quite a few of these kind of questions - in a much smaller version, of course - in math these few days so completely SICK of it.)
Thu Mar 31, 2005 10:04 pm
Wow. I got a huge number. x_x
Thu Mar 31, 2005 10:11 pm
19 digits long o_0? 
They always said skeiths werent so bright... i upset than I didnt know the dimentions of an armada board... and thus that part took me half of the time. Still solve in under 15 minuts... does that mean I get a silver trophey?
They always said skeiths werent so bright... i upset than I didnt know the dimentions of an armada board... and thus that part took me half of the time. Still solve in under 15 minuts... does that mean I get a silver trophey?
Thu Mar 31, 2005 10:29 pm
i got an answer.. not sure if its right.. id like to confirm